2021. 6. 14. 11:44ㆍAI-딥러닝/딥러닝
딥러닝에서 오차를 차례차례 이전 층으로 전파시켜 가중치와 편향을 조금씩 수정하면서 최적화하기 위해서 “경사하강법”이라는 알고리즘을 이용합니다.
이 글에서는 경사하강법의 개념과 경사하강법을 위한 미분에 대해서 알아보겠습니다.
<경사하강법>
경사하강법이란, 어떤 파라미터 x_k 의 변화량에 대한 함수 y(x_(1, ), x_2, x_3, …..x_k, …)의 변화율
즉 기울기 ∂y/(∂x_k )를 구해 이 기울기에 따라 파라미터를 조정하고 y를 최적화하는 알고리즘을 경사하강법 이라고 합니다.
경사 하강법은 경사법의 한 종류로서 결과가 y의 최솟값을 향해 내려가도록 파라미터 x_k를 변화시킵니다.
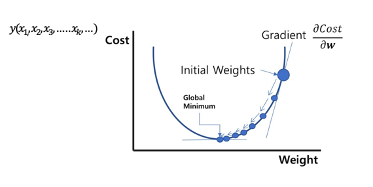
여기서 우리가 이전 글에서 배운 역전파를 생각하면 다음과 같은 생각을 할 수 있을겁니다.
역전파에서 손실함수로 구한 오차값을 기점으로 신경망의 반대 방향으로 가중치와 편향을 수정해 나가는데 이때 경사하강법으로 수정량을 결정합니다.
경사 하강법에서는 오차가 줄어들도록 가중치와 오차를 조정합니다.
역전파에서 경사 하강법은 밑에 그림을 같이 보면 이해하는데 도움이 될 것 같습니다.
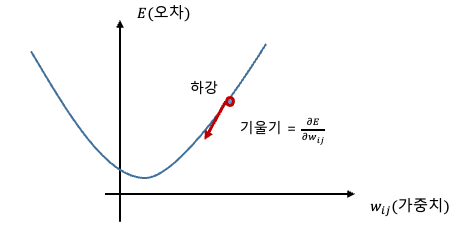
하강하면서 오차를 계산하고 기울기를 조절하게 되는겁니다.
그래프에서 가로축 w_ij는 가중치, 세로축은 E는 오차 입니다.
가중치에 따라 오차가 변하는데 실제로는 이렇게 곡선의 형태를 알기 어렵기 때문에 오차가 최소가 되는 방향으로 조금씩 가중치를 변화 시켜갑니다.
이 때 각 가중치(뉴런마다 들어오는 값들의 가중치)의 변화량은 이 곡선의 기울기로 결정됩니다. 편향(bias)도 마찬가지입니다.
따라서 신경망의 모든 가중치와 편향을 수정하기 위해 우선 필요한 것은 모든 가중치와 편향에 대한 오차의 기울기를 구하는 것입니다.
위 그림은 단순한 2차원형태의 그림이지만
해결하려는 문제의 난이도에 따라 그래프는 복잡해 질 수 있습니다. w_ij의 변화에 대한 E의 변화는 반드시 위 그래프처럼만 그려지는 것은 아닙니다. 여러 가지 상황에 따라 그려지는 모양이 달라집니다.
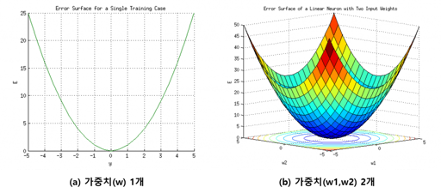
아래 그림 처럼도 그려질 수 있습니다.
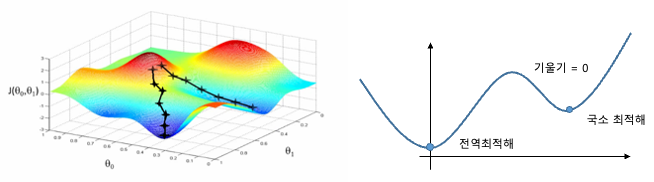
위 그림을 보면 "국소최적해"라고 적혀 있는 것을 볼 수 있습니다.
국소 최적해란 최소점에 빠져 더 이상 가중치 수정을 하지 않고 전체 최솟값에 도달하지 못하는 경우를 의미합니다. 이런 경우 학습률이 오르지 않고 원인을 분석하여 빠져나와야합니다.
전역최적해는 쉽게 풀이하여 국소최적해의 반대인 정답에 도착하는 기울기를 구하여 도착한 최종목적지 입니다.
'AI-딥러닝 > 딥러닝' 카테고리의 다른 글
| 딥러닝 - 회귀에서의 역전파 구현 (0) | 2021.06.14 |
|---|---|
| 딥러닝 - 경사하강법 기울기 연산 (0) | 2021.06.14 |
| 딥러닝 - 손실함수 (0) | 2021.06.14 |
| 딥러닝 - 역전파(back propagation) (0) | 2021.06.14 |
| 딥러닝 - 활성화 함수 (0) | 2021.06.14 |