2021. 6. 14. 01:20ㆍAI-딥러닝/딥러닝
딥러닝의 순저파에 대해 공부하고 정리해보고자 한다.
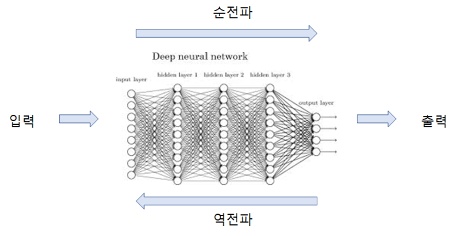
순전파시에 각 뉴런에서 일어나는 수식 계산들을 수식화하여 설명해보고자 한다.
만약, 다음과 같은 신경망이 존재한다고 가정하자.
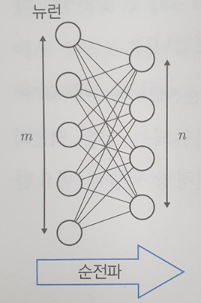
일단 위 신경망을 설명하면,
앞 층의 모든 뉴런은 뒤 층의 모든 뉴런과 연결되어 있다고 가정하고,
반대로 뒤 층의 모든 뉴런이 앞 층의 모든 뉴런과 연결되어 있다고 가정,
그러면 가중치의 개수와 입력의 수가 일치함으로 앞 층 뉴런의 수를 m이라고 한다면 뒤 층 뉴런의 1개는 m개의 가중치를 갖게 됩니다.
즉, 뒤 층 뉴런의 총수를 n이라고 하면 뒤 층에는 m ∗n개의 가중치가 존재하게 됩니다.
1.
그럼 다음과 같이 m * n 행렬은 뒤 층의 모든 가중치를 행렬로 표시가 가능합니다.

또한 앞 층의 출력(= 뒤 층의 입력)은 벡터로 표시할 수 있으며, 앞 층에 m개의 뉴런이 있으므로 벡터의 원소 개수는 m이 됩니다.
앞 층의 출력을 y ⃑ 뒤 층의 입력을 x ⃑로 표시하면 다음과 같이 표시할 수 있다.

2. 1번에서 설명대로 한다면 편향(bias)도 벡터로 표형할 수 있고, 편향 개수는 뒤 층 뉴런의 개수와 같고, 뒤 층 뉴런 개수가 n과 동일하므로 벡터 (b_j ) ⃑ 는 다음과 같이 표시할 수 있습니다.

3. 출력 수 또한 뉴런의 수 n과 동일함으로 벡터 (y_j ) ⃑를 이용해 다음과 같이 표기할 수 있습니다.
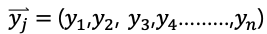
4. 앞 단일 뉴런에서 했던 출력을 위해 했던 과정을 뉴런네트워크에 적용하여 수식화 해보겠습니다. (앞 층에서 하나의 뉴런의 출력값이 뒤 층의 입력이라고 가정)

5. 4번에서 의 계산에 편향값((b_j ) ⃑)을 더한 것을 ( u) ⃑ 라고 하면, ( u_j ) ⃑는 다음과 같습니다.

6. 위에서 계산한 일련의 과정을 (u_j ) ⃑는 넘파이의 dot 함수를 이용하여 다음과 같이 계산할 수 있습니다.

7. 4번에서 의 계산에 편향값((b_j ) ⃑)을 더한 것을 ( u) ⃑ 라고 하면, ( u_j ) ⃑는 활성함수 f(x)에 넣어서 표현하면 다음과 같습니다.
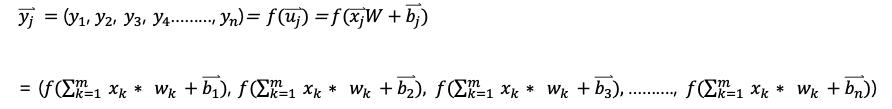
딥러닝을 구현하는데 위 개념이 꼭 필요하지는 않은거 같지만, 이 과정을 이해하면 "활성화 함수"와 "역전파"시에 더 정확한 딥러닝이 어떻게 하면 나올 수 있겠구나라는 생각을 할 수 있었던 것 같습니다.
꼭 한번 보고 넘어가면 좋은 내용일 것 같습니다.
'AI-딥러닝 > 딥러닝' 카테고리의 다른 글
| 딥러닝 - 역전파(back propagation) (0) | 2021.06.14 |
|---|---|
| 딥러닝 - 활성화 함수 (0) | 2021.06.14 |
| 딥러닝 - 뉴런을 모아 네트워크화 (0) | 2021.06.13 |
| 딥러닝 - 뉴런 (0) | 2021.06.13 |
| 머신러닝의 학습 방식 및 방법 (0) | 2021.05.14 |